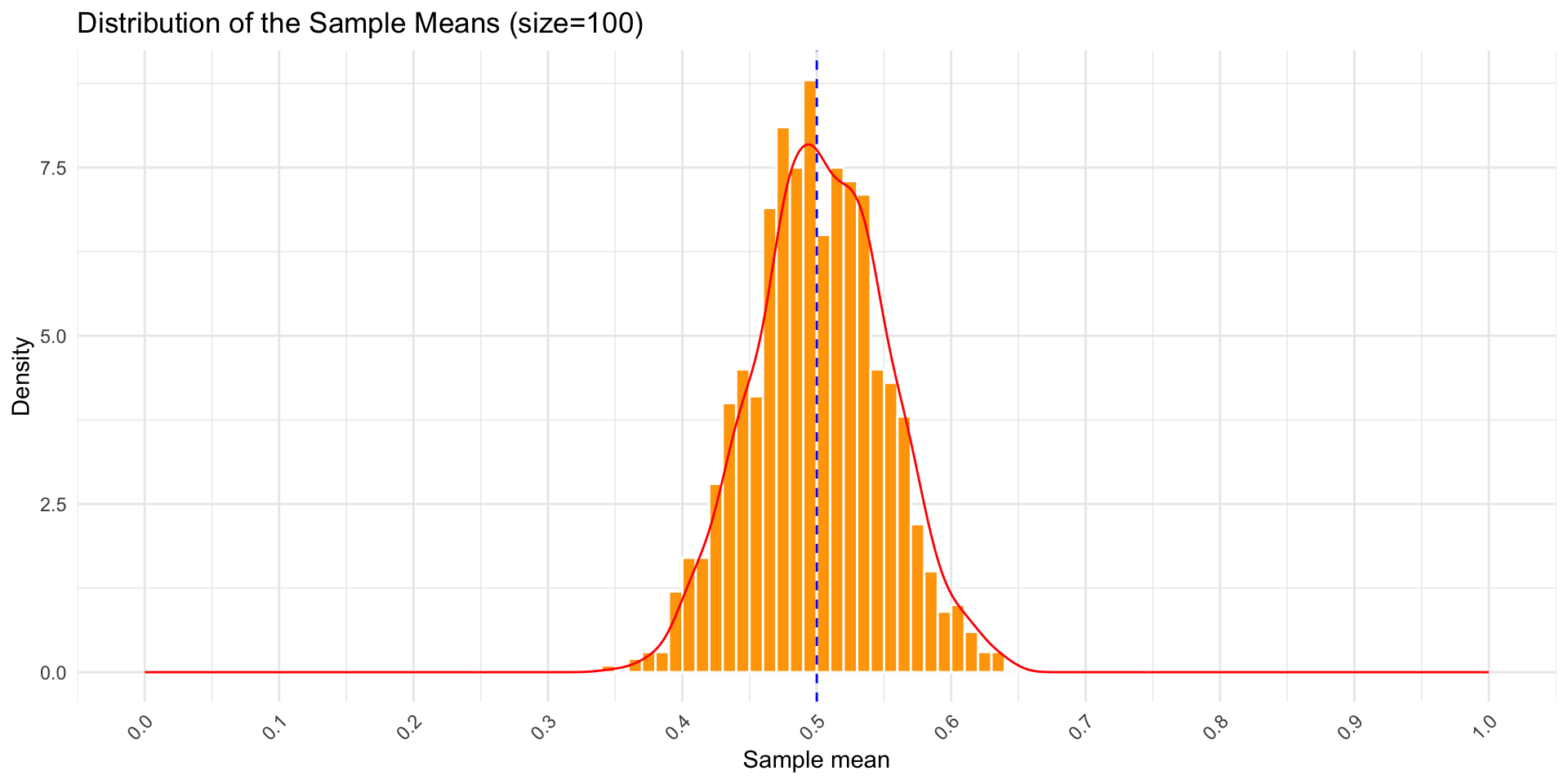
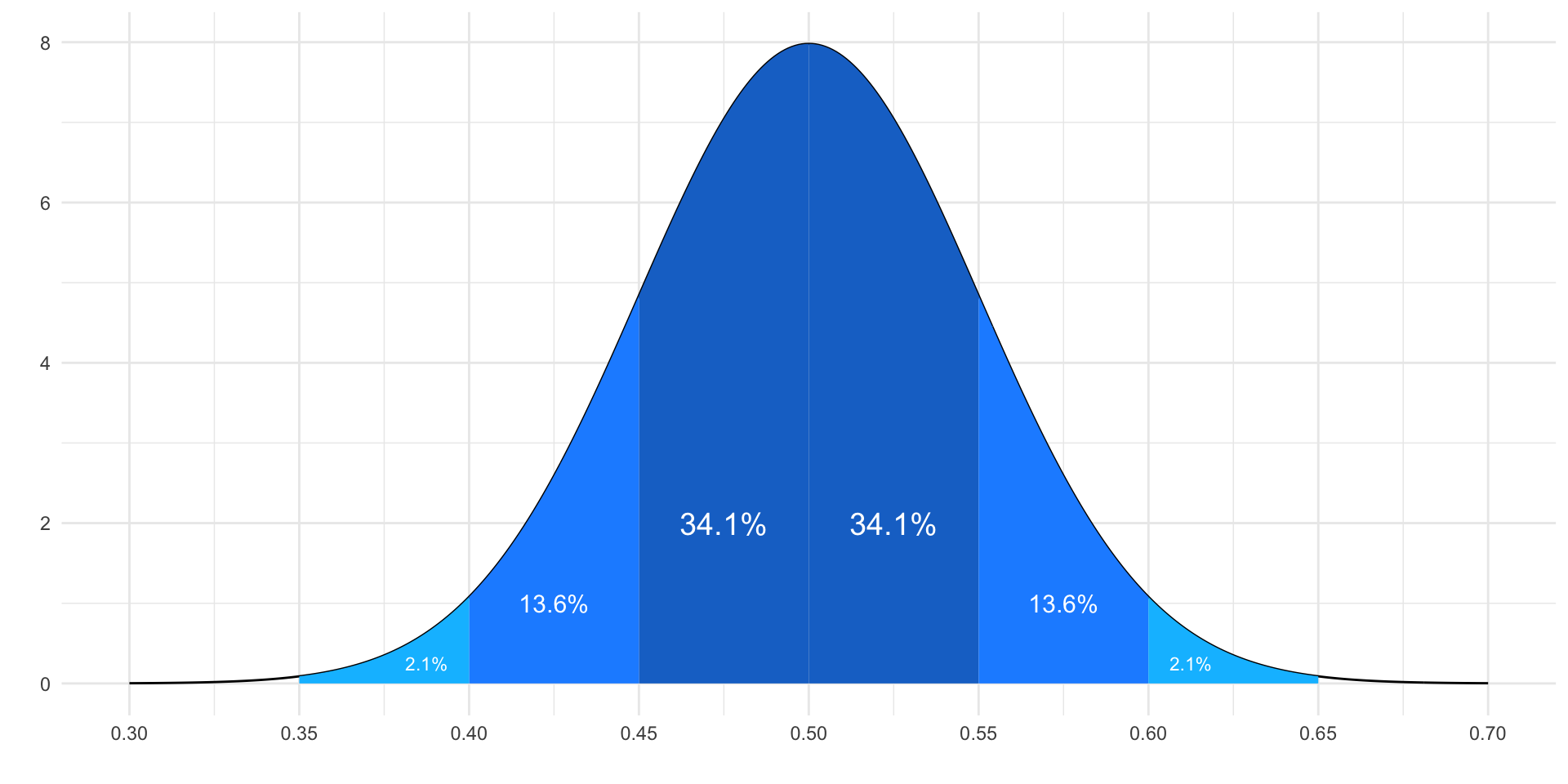
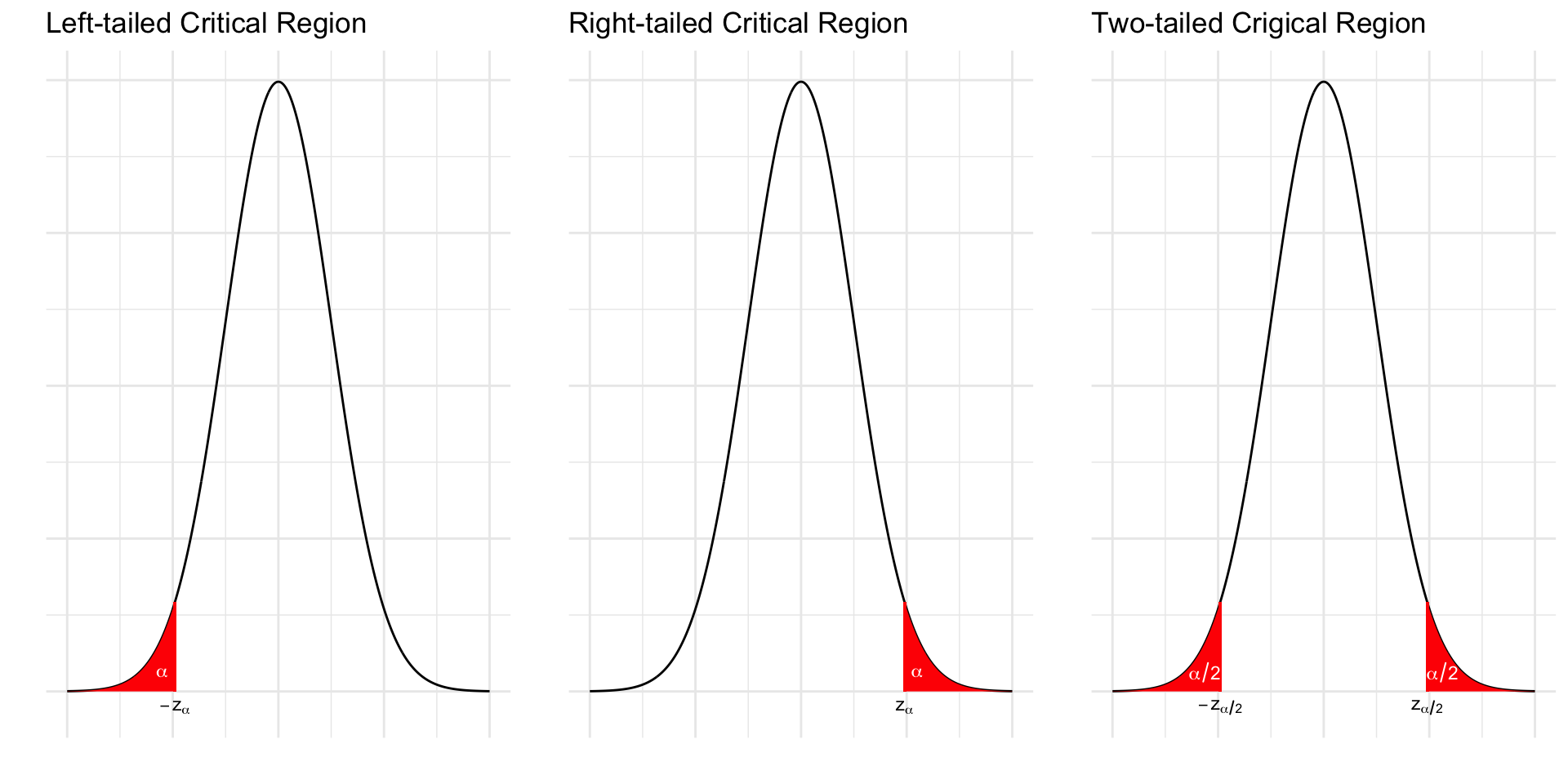
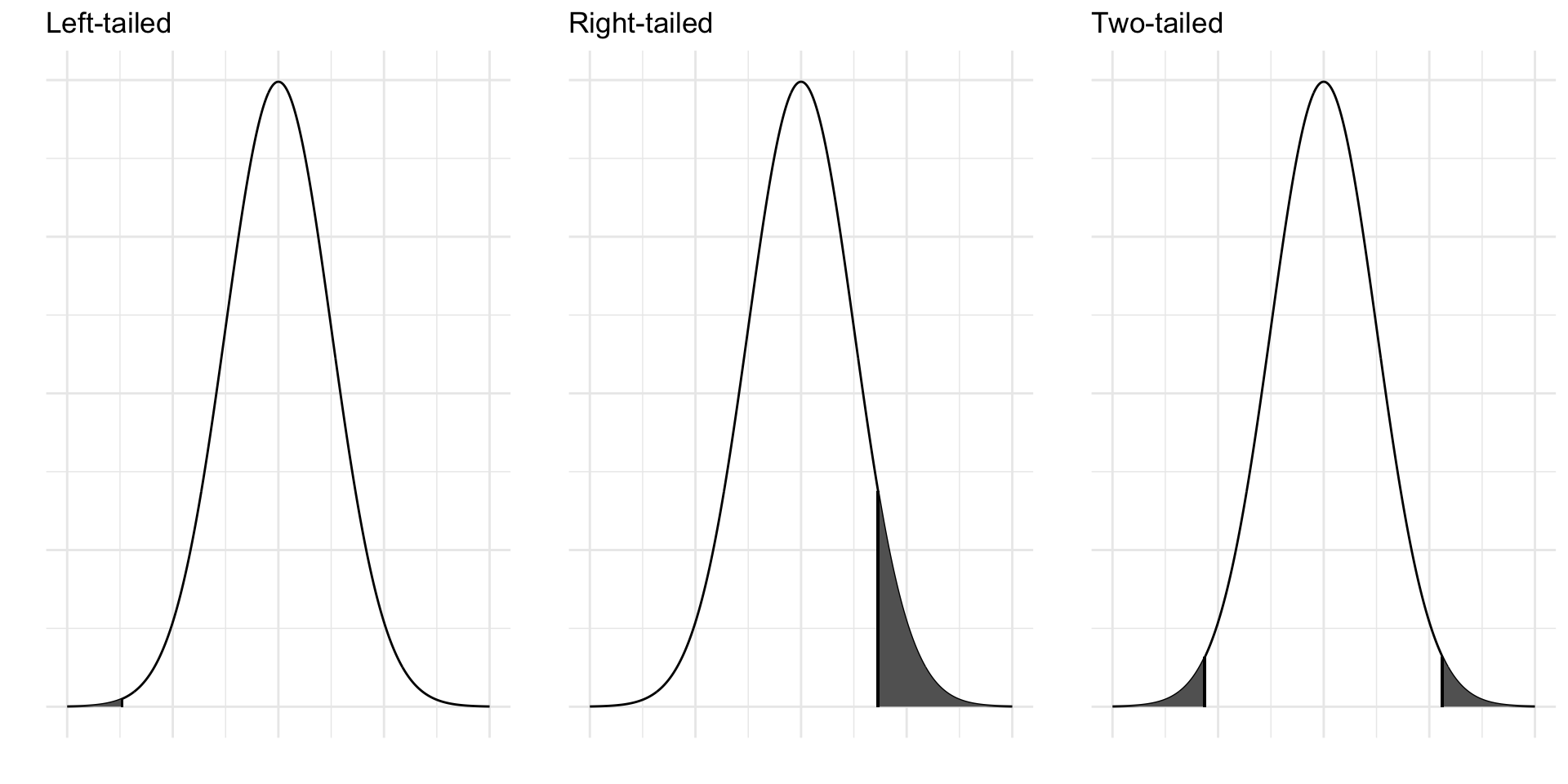
library(tidyverse)
source("../utils.R")
red_marble = "🔴"
blue_marble = "🔵"
prob_red = 0.64
num_marbles = 5000
set.seed(42)
marbles = sample(c(red_marble, blue_marble), size = num_marbles,
replace = TRUE, prob = c(prob_red, 1 - prob_red))
set.seed(42)
n = 100
one_sample = sample(marbles, n)
p_hat = mean(one_sample == red_marble)
print(str_glue("Percentage of red marbles: {p_hat * 100}%"))Percentage of red marbles: 69%