Unraveling the Confidence Interval Puzzle

From a Single Estimate to a Range

Central Limit Theorem

As the sample size increases, typically when it’s greater than 30, the distribution of the sample means approaches a normal distribution.

Mathematically,

\[\bar X \sim N(\mu, \frac{\sigma^2}{n})\]

where \(\mu\) is the population mean and \(\sigma^2\) is the population variance.

Red Marble Proportion Estimation

library(tidyverse)
source("../utils.R")

red_marble = "🔴"
blue_marble = "🔵"

prob_red = 0.64
num_marbles = 5000 # 1000 -> 5000

set.seed(42)
marbles = sample(c(red_marble, blue_marble), size = num_marbles, 
                 replace = TRUE, prob = c(prob_red, 1 - prob_red))

set.seed(42)
n = 100
one_sample = sample(marbles, n)
print(str_glue("Percentage of red marbles: {mean(one_sample == red_marble) * 100}%"))

Percentage of red marbles: 69%

• How confident are we in the estimation?
• How can we quantify our level of certainty?

Confidence Interval

“The proportion of red marbles is exactly 69%.”

Confidence Interval

“The proportion of red marbles is exactly 69%.”

“I am 95% confident the proportion of red marbles in the bag is between 59% and 79%, which is also can be written as 69% \(\pm\) 10%.”

Margin of Error

\[\text{Margin of Error} = \text{Critical Value} \times \text{Standard Error}\]

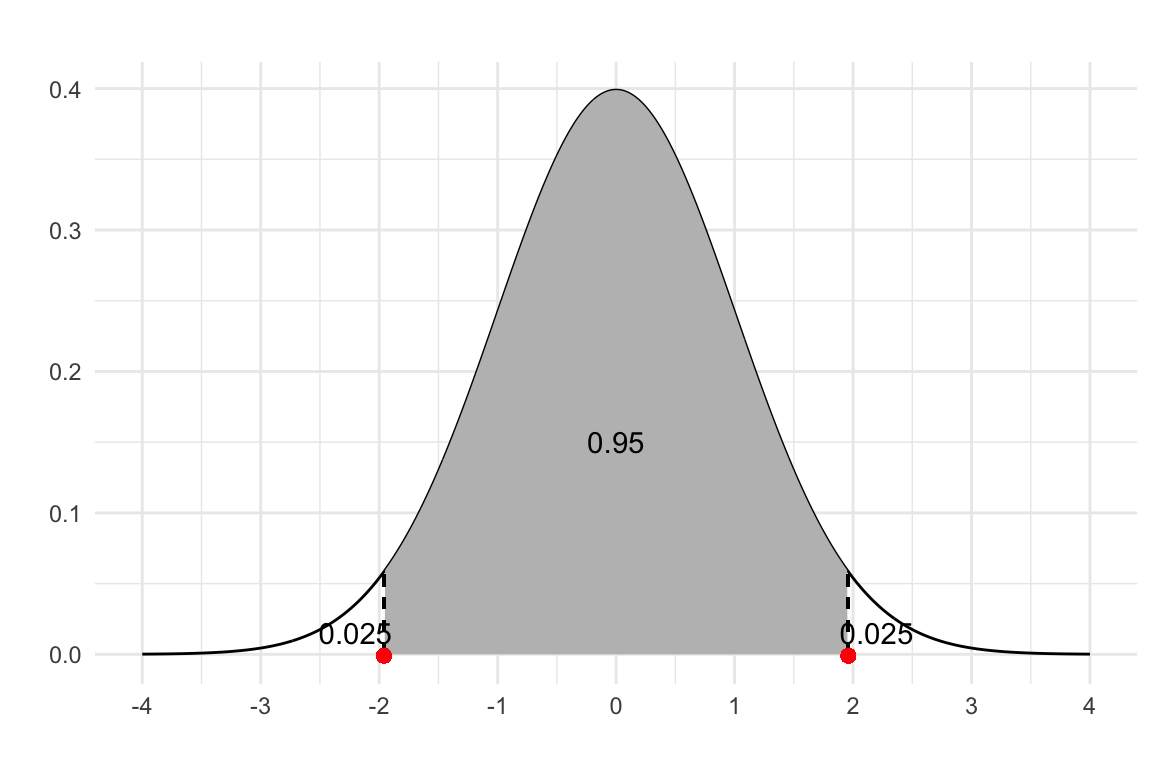
Critical Value (\(z\)-score)

A \(z\)-score indicates how many standard deviations a data point is from the mean of the dataset.

Calculating \(z\)-score

z_95 = qnorm(1 - 0.05 / 2)
print(str_glue("z score for 95% confidence level: {round(z_95, 2)}"))

z score for 95% confidence level: 1.96

Standard Error

Population Variance Known

\[SE = \frac{\sigma}{\sqrt{n}}\]

Population Variance Unknown

\[SE_{\hat p} = \sqrt{\frac{\hat p (1 - \hat p)}{n}}\]

where \(\hat p\) is the sample proportion.

p_hat = mean(one_sample == red_marble)
print(str_glue("Sample Proportion: {p_hat}"))

Sample Proportion: 0.69

se = sqrt(p_hat * (1 - p_hat) / n)
print(str_glue("Standard Error: {round(se, 3)}"))

Standard Error: 0.046

Margin of Error (MOE)

\[MOE = z \times SE\]

moe = z_95 * se
print(str_glue("Margin of Error: {round(moe, 3)}"))

Margin of Error: 0.091

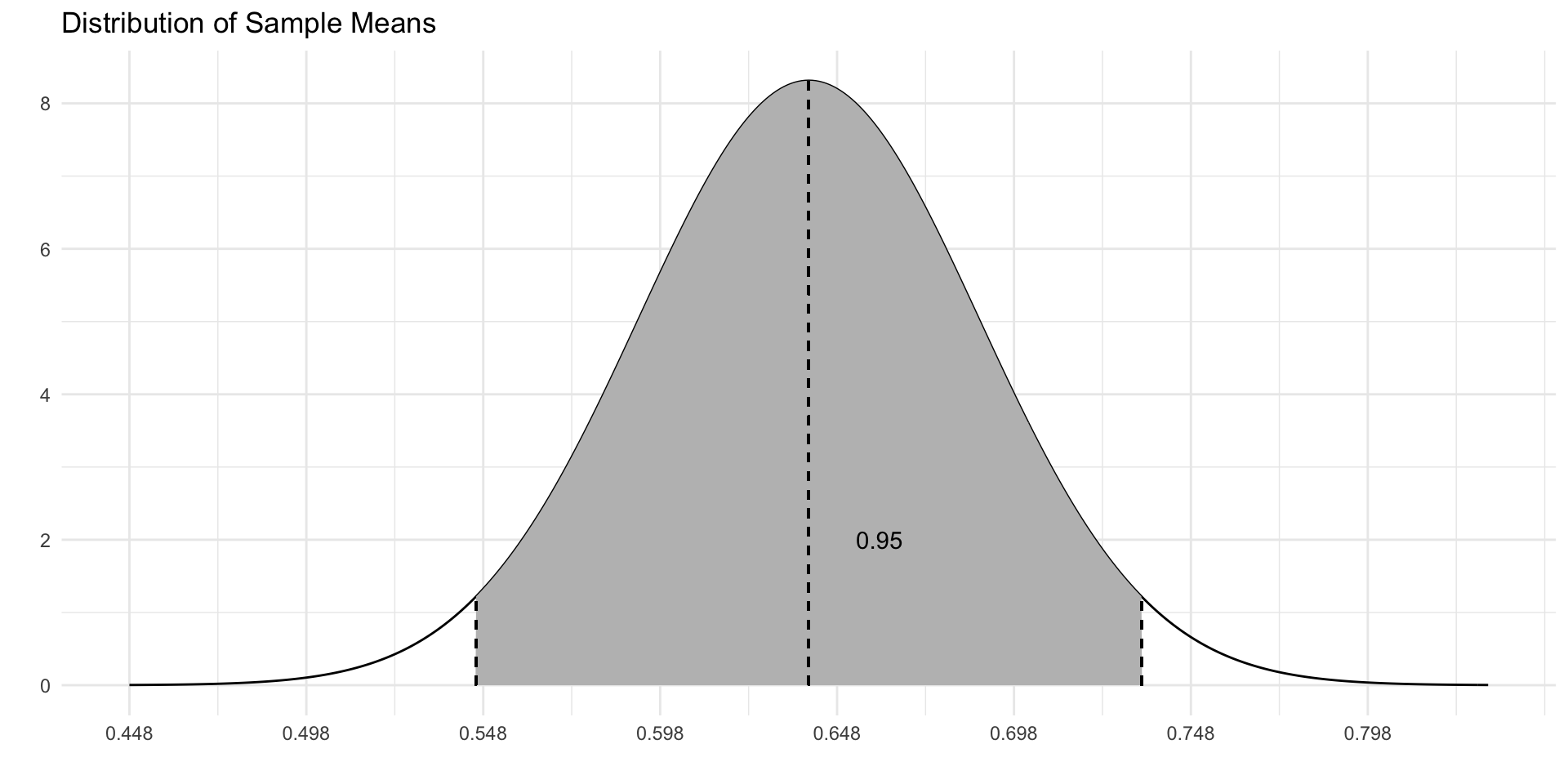
95% Confidence Interval

\[CI = (\hat p - MOE, \hat p + MOE)\]

lower_limit = p_hat - moe
upper_limit = p_hat + moe
print(str_glue("95% CI: [{round(lower_limit, 3)}, {round(upper_limit, 3)}]"))

95% CI: [0.599, 0.781]

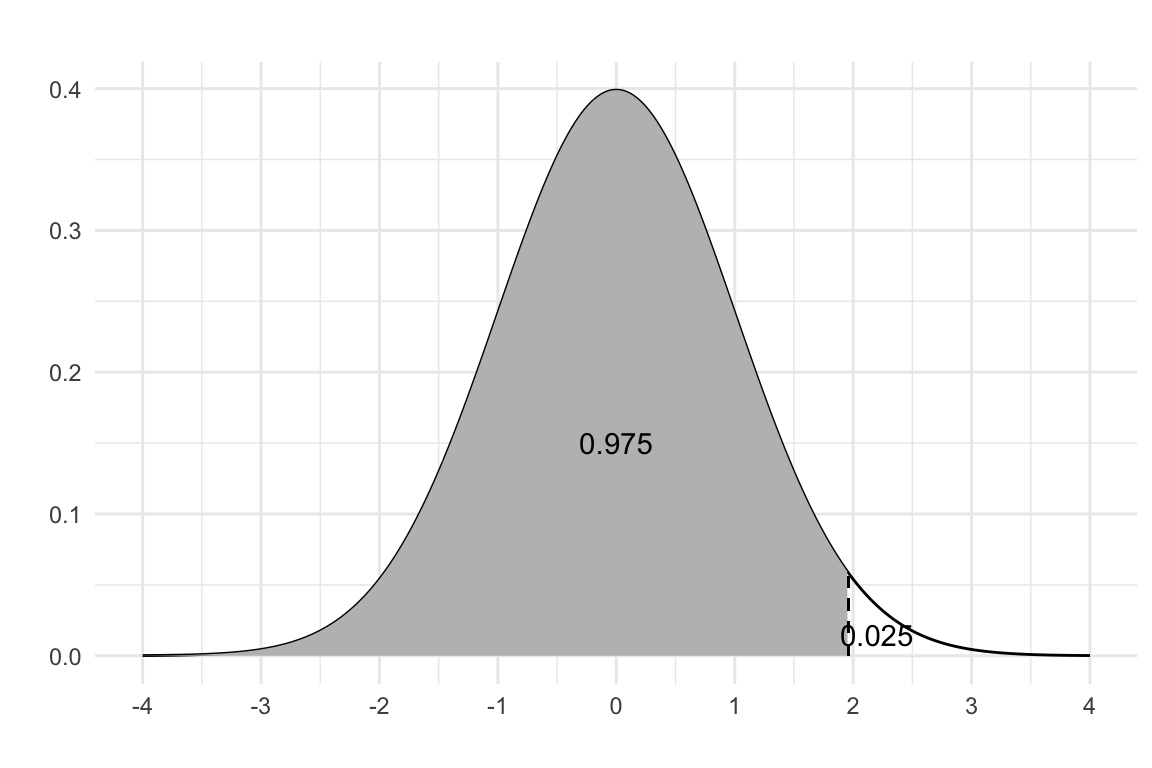
99% Confidence Interval

z_99 = qnorm(1 - 0.01 / 2)
moe = z_99 * se
lower_limit = p_hat - moe
upper_limit = p_hat + moe
print(str_glue("99% CI: [{round(lower_limit, 3)}, {round(upper_limit, 3)}]"))

99% CI: [0.571, 0.809]

How it works?

How it works?

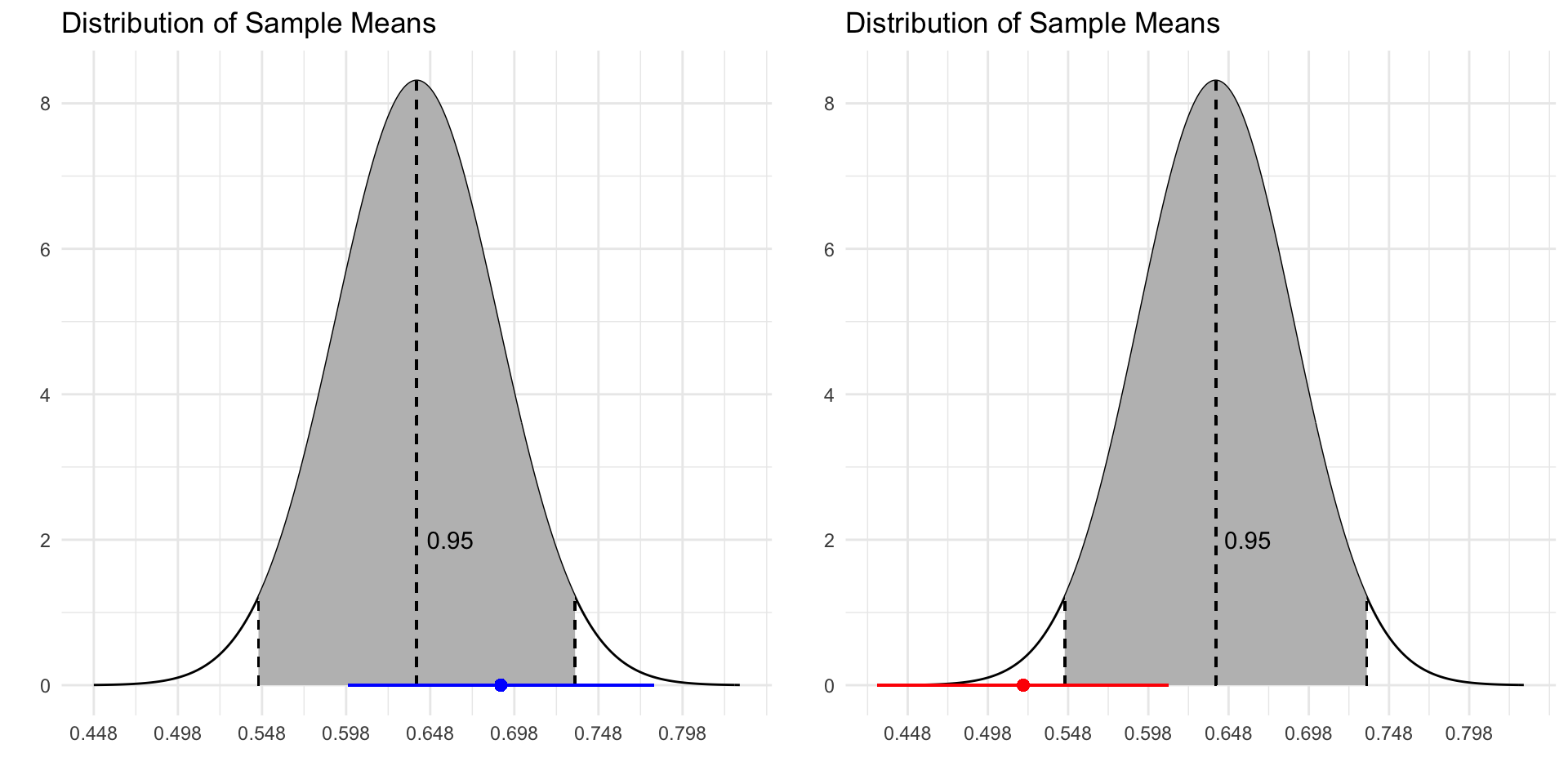
Confidence Level

A 95% confidence level means that if we were to take the samples and construct a confidence interval from each sample, we are expecting that the intervals would capture the true population mean about 95% of the time.

95% Confidence Level

Steps for Constructing CI

• Compute the sample proportion, \(\hat p\)
• Find critical value, \(z\), corresponding to the confidence level
• Compute the standard error, \(SE = \sqrt{\hat p (1 - \hat p) / n}\)
• Compute the Margin of Error, \(MOE = z\times SE\)
• Construct confidence interval, \(\hat p \pm MOE\)

Question

“Half of the marbles in the bag are red!”